
No terceiro nível, a obra analisada foi uma pintura abstrata da autoria de Jorge Pinheiro. Como observou a guia da exposição, para interpretar este quadro era necessário ter alguns conhecimentos de Matemática, sem os quais não era possível entender as ideias que o pintor pretendeu transmitir.
O pintor desenhou um quadro que representava algumas das ideias do matemático italiano (do século XIII), Leonardo de Pisa, conhecido por Fibonacci. Este matemático colocou um problema prático que consistia em calcular quantos coelhos seriam gerados num ano a partir de um único casal. Supondo que cada casal leva um mês, após nascer, para ficar fértil e gera sempre outro casal a cada mês, e que nenhum coelho morre durante o ano, Fibonacci chegou a uma sequência que correspondia ao número de coelhos gerados em cada mês:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377...
Nesta sequência de números naturais, podemos obter um termo qualquer da sequência, a partir do 3º, somando os dois termos imediatamente anteriores a ele. Por exemplo, 3 = 2 + 1; 34 = 21 + 13, etc. Supondo, hipoteticamente, que os coelhos tinham vida eterna, esta sequência seria infinita.
Além disso, a razão de semelhança entre um número e o seu precedente (a partir do 5º termo da sequência) está sempre próxima de 1,6 (valor aproximado do "número de ouro": 5/3=1,666....; 8/5 = 1,6; 13/8 = 1,625 e assim por diante), este número é um limite, tende para 1.68.
Para exemplificar uma das aplicações da sequência de Fibonacci, as guias da exposição recortaram numa folha A3 uma série de figuras geométricas, de acordo com as proporções a seguir descritas nas imagens.
Fotografia de Samuel Camacho do 11º F.
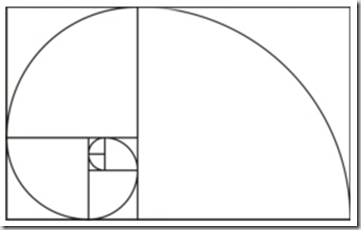
Como se pode observar na imagem anterior, a folha recortada tinha desenhado o seguinte: de dois quadrados de lado 1, obteve-se um rectângulo de lados 2 e 1. Adicionando a esse rectângulo um quadrado de lado 2, obteve-se um novo rectângulo 3×2. Adicionando um quadrado de lado 3, obteve-se um rectângulo 5×3. Observando a figura, vemos que os lados dos quadrados adicionados para determinar os rectângulos formam a sequência de Fibonacci.
Se utilizarmos um compasso e traçarmos o quarto de circunferência inscrito em cada quadrado, encontraremos uma espiral formada pela concordância de arcos cujos raios são os elementos da sequência de Fibonacci.
Ao rectângulo anterior chama-se rectângulo áureo ou rectângulo de ouro. Este tem uma particularidade: a razão entre o maior e o menor lado é igual ao número Φ, fi, (também conhecido como “proporção áurea” ou "número de ouro") que corresponde a 1,6180339887....(para saber mais, ver os slides disponibilizados no final).
O número fi pode ser encontrado em padrões matemáticos, físicos e biológicos. Além disso, foi também usado como referência estética nas artes plásticas. No mundo vegetal e animal, o número fi e a sequência de Fibonacci surgem em muitas situações, como por exemplo, nas espirais das conchas (nautilos) e da casca do abacaxi (para conhecer outros exemplos, ver aqui).
Georgeta, Jéssica e Tatiana, 11º C
Para quem quiser saber MAIS sobre a sequência de Fibonacci, consultar a informação disponibilizada nos slides seguintes.


Sem comentários:
Enviar um comentário